Rethinking Incremental and Parallel Pointer Analysis
Rethinking Incremental and Parallel Pointer Analysis来自TOPLAS,介绍了一种增量的可并行的指针分析算法。
Abstract
本文介绍了基于Andersen’s Analysis实现的增量指针分析算法。
1 | 1 Δ1 ← ∅;// Δ1: the new points-to constraints in each iteration |
代码的变化总是可以用插入(insertion)和删除(deletion)两种动作来表示。
对于现实世界的代码,Andersen分析可以动态的构建PAG(Pointer Assignment Graph)。那么这种动态构建结果的能力可以直接作用于insertion,即提取新增代码对于指针分析的作用,然后重新执行on-the-fly algorithm进行计算。
而对于deletion的处理则要复杂许多。需要维护出处信息,用于在语句被删除是,做出对应的变更。
现有的应对deletion的处理方法基本可以分为两类:
reset-recompute,例如:reachability based,例如:
Reset-Recompute Algorithm
最直接的思路就是当发生删除操作时,对关联变量的points-to set进行重置和重算,所谓关联就是在PAG上从被删除的根节点出发可达的节点。该方法的问题在于对于需要重置节点的计算大多数情况下可能是冗余的,导致效率不高。
此外针对这种算法发展出了基于IDE/IFDS框架的优化和基于Graph-Pattern的优化方法。
Reachability-Based Algorithm
该做法突出一个updated lazily的概念,可能受到删除影响的节点不会立刻被重置,当切仅当它们不能从删除的语句所表示的相应内存对象可达时才会被更新。这种做法同样相当费时,可达性计算的成本会随着PAG图的规模而增加。
New Incremental Algorithm
新的算法通过识别哪些是当deletion发生时,哪些PAG中的节点需要被更新,并及时停止更新的传递来减少冗余计算,同时证明了实现并行的可能。
首先需要通过Strongly Connected Components(SCC)优化实现PAG中的去环。因为对于SCC中的节点,points-to set是无效的,那么它们可以塌缩成一个单独的节点,以此保证PAG中无环。
在一个无环的PAG中,可以得到以下两个性质
Lemma 1 [Incoming Neighbors Property]. Consider an acyclic PAG and a pointer node q of which an object o ∈ pts (q). If q has an incoming neighbor r (that is, there exists an edge r →q) and o ∈ pts (r ), then there must exist a path from o to r without going through q.
这条可以推导出,当对象O属于Q的指向集合,如果删除一条从Q指向P的边,如果P的其他incoming neighbor不包含对象O,那么O可以从P的指向集中删除。这说明当某条边被删除时,我们只需要check这条边终点的incoming neighbor
Lemma 2 [Outgoing Neighbors Property]. Consider an acyclic PAG and a pointer node q of which an object o ∈ pts (q). Assume that q has an outgoing neighbor w (i.e., there exists an edge q → w) and w has an incoming neighbor r (different from q) such that o ∈ pts (r ). If r cannot reach q, then at least one of the following two conditions (or both) must hold in the PAG:
(1) There exists a path from o to w without going through q.
(2) There exists a path from q to r .
即对于p -> q -> w的情况,如果删除p->q并且o从q的指向集中删除,那么对于作为q的outgoing neighbors的w而言,需要检查它的incoming neighbors,如果incoming neighbors的指向集中仍然含有o,那么传播终止。
基于上述结论,设计了新的算法来增量处理deletion的情况。

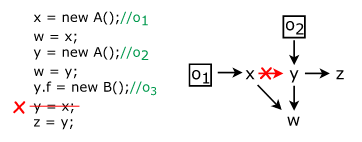
举例说明,PAG如下图所示,当删除掉x -> y这条边:
- 由于
y的其他入度不包含o1,所以o1可以从y的指向集中删除(Lemma 1); - 继续考察
y的出度:- 对于
z,由于z的其他入度同样不包含o1,所以同样删除; - 对于
w,存在一条o1 -> x -> w的路径,所以这个修改会被跳过,并且终止传播(Lemma 2);
- 对于
Parallel
Lemma 3 [Change Idempotency Property]. For an edge insertion or deletion, the update to each points-to set is an idempotent operator. In other words, if the change propagates to a node more than once from different paths, the effect of the change (i.e., the modification applied to the corresponding points-to set) must be the same.
这条性质类似于幂等性?!这保证了对于一个修改的不同路径进行并行化传播,并不会发生冲突,如下图:
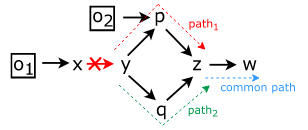
无论路径一或路径二的先后顺序如何,都不会影响最终的结果。
DISCUSSIONS
- Flow sensitivity
没有选择flow-sensitivity的原因在于,需要同时维护control-flow的变化,而control-flow和data-flow的分析并不是正交的,特别是高精度的control-flow graph和points-to analysis通常是相互递归的。
- Context sensitivity
由于对于context而言PAG中edge的增加和删除都是正交的,所以完全可以改造成上下文敏感分析。
图片数据、伪代码来源 Rethinking Incremental and Parallel Pointer Analysis